El problema de Josephus
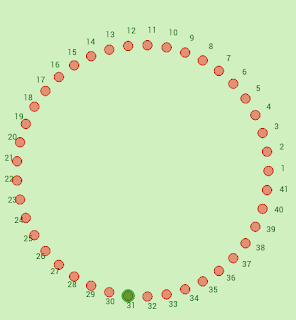
El problema de Flavio Josefo es un problema teórico que se encuentra en matemáticas y ciencias informáticas. El nombre hace referencia a Flavio Josefo, un historiador judío que vivió en el siglo I. Según lo que cuenta Josefo, él y 40 soldados camaradas se encontraban atrapados en una cueva, rodeados de romanos. Prefirieron suicidarse antes que ser capturados y decidieron que echarían a suertes quién mataba a quién. Los últimos que quedaron fueron él y otro hombre. Entonces convenció al otro hombre que debían entregarse a los romanos en lugar de matarse entre ellos. Josefo atribuyó su supervivencia a la suerte o a la Providencia. El planteamiento general del problema, presupone cualquier número de soldados, n, y un valor k que indica el salto en cada "asesinato". Por ejemplo, si empieza en el número 1 y k = 3, el primero en desaparecer sería el número 4. Es un clásico problema que se resuelve en los estudios de Programación en cualquier lenguaje. La forma gener